Autora:Sirley Peñafiel Galarza
La radicación se define como la operación inversa de la potenciación, y consiste en que dados dos números, llamados radicando e índice, hallar un tercero, llamado raíz, tal que, elevado al índice, sea igual al radicando.
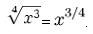
Veremos ahora las propiedades de la radicación:
• Es distributiva con respecto a la multiplicación y a la división.
Veamos un ejemplo:
En la división
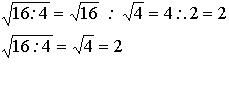
En la multiplicación
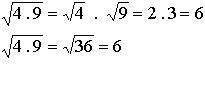
• No es distributiva con respecto a la suma y a la resta.
Ejemplos:
En la suma
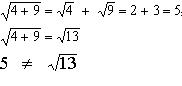
En la resta
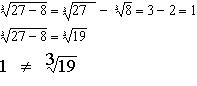
Para sacar la raíz de un cierto número (radicando), buscamos el número que elevado al índice me de por resultado el radicando.
Si
el índice es par entonces el radicado tiene que
ser positivo y la raíz tiene dos resultados, uno positivo y otro
negativo, para este nivel usamos el resultado positivo.
EJEMPLO:

Si el índice es impar entonces la raíz va a tener el mismo signo que el radicando.
EJEMPLO:

Si tengo una raíz de raíz se multiplican los índices.
EJEMPLO:

RECURSOS MULTIMEDIAS
RECURSO INTERACTIVO PARA PRACTICAR
TALLER:
REFERENCIAS DE TEXTO:
REFERENCIAS MULTIMEDIA: